
OP-DLC 2 : Great Truths are Always Simple !
1. Introduction
Discreet Log Contract (DLC) is a contract execution framework based on Oracles, proposed by Tadge Dryja from MIT in 2018. DLC allows two parties to make conditional payments based on predefined conditions. The parties predetermine possible outcomes and pre-sign them, and then use these pre-signed agreements to execute payments when the Oracle signs off on the result. Thus, DLC ensures the security of Bitcoin deposits while enabling new decentralized financial applications.
The previous article, “DLC and Its Optimization Considerations”, summarized the advantages of DLC in terms of privacy protection, complex contracts, and low asset risk. It also analyzed issues such as key risks, decentralized trust risks, and collusion risks within DLC. To address these problems, decentralized Oracles, threshold signatures, and optimistic challenge mechanisms were introduced into DLC. Given that DLC involves three participants—Oracle, Alice, and Bob—the exhaustive attack scenarios among different participants are relatively complex, leading to equally complex preventive strategies. These complicated defense strategies are not perfect, as they do not adhere to the principle of simplicity and lack the elegance of simplicity.
In Bitcoin, any action by any participant must be realized through UTXO (Unspent Transaction Output). Therefore, using a consensus mechanism to ensure the correctness of UTXO can resist any attack. Similarly, in DLC, any action by any participant must be realized through CET (Contract Execution Transaction). Thus, using an optimistic challenge mechanism to ensure the correctness of CET can resist any attack. Specifically, the Oracle can sign the CET after staking 2 BTC. An optimistic challenge mechanism is added to CET. If a CET is not challenged or successfully counters a challenge, the CET is deemed correct and can be settled, allowing the Oracle to release its stake and receive a fee. If the Oracle attempts to act maliciously, anyone can successfully challenge it, preventing the CET from being settled. In this case, the Oracle loses its stake and can no longer sign the same CET. This approach adheres to the principle of simplicity and embodies elegant simplicity.
2. DLC Principle
Alice and Bob sign a betting agreement: they wager on whether the hash value of the ξ-th block is odd or even. If it is odd, Alice wins the game and can withdraw the assets; if it is even, Bob wins the game and can withdraw the assets. Using DLC, the Oracle transmits the information of the ξ-th block to construct conditional signatures, ensuring that the correct winner gains all the assets.
The elliptic curve generator is G, with order q. The key pairs for Oracle, Alice, and Bob are (z, Z), (x, X), (y, Y) respectively.
Funding transaction (on-chain): Alice and Bob jointly create a funding transaction, each locking 10 BTC in a 2-of-2 multi-signature output (public key X belongs to Alice, and public key Y belongs to Bob).
Constructing CET (off-chain): Alice and Bob create CET1 and CET2 for spending the funding transaction output. The Oracle computes the commitment R = k · G, and then calculates S and S’ as follows:
\[S := R - hash(OddNumber, R) · Z,\] \[S' := R - hash(EvenNumber, R) · Z.\]The new public keys for Alice and Bob are as follows:
\[PK^{Alice} := X + S,\] \[PK^{Bob} := Y + S'.\]Settlement (off-chain to on-chain): When the ξ-th block is successfully generated, the Oracle signs the corresponding CET1 or CET2 based on the hash value of that block.
If the hash is odd, the Oracle signs as follows:
\[s := k - hash(OddNumber, R) z.\]Broadcasts CET1.
If the hash is even, the Oracle signs as follows:
\[s' := k - hash(EvenNumber, R) z.\]Broadcasts CET2.
Withdrawal (on-chain): If the Oracle broadcasts CET1, Alice can compute the new private key and spend the locked 20 BTC
\[sk^{Alice} = x + s.\]If the Oracle broadcasts CET2, Bob can compute the new private key and spend the locked 20 BTC
\[sk^{Bob} = y + s'.\]The Bitlayer research group found that in the above process, any action needs to be realized through CET. Therefore, using an optimistic challenge mechanism to ensure the correctness of CET can resist any attack. Incorrect CETs will be challenged and not executed, while correct CETs will be executed. Additionally, the Oracle must pay the price for malicious behavior.
For a challenge program denoted as f(t), the CET should be constructed as follows
\[s = k - hash(f(t), R) z.\]Suppose the actual situation is that the hash value of the ξ-th block is odd, i.e., f(ξ) = OddNumber, the Oracle should sign CET1
\[s := k - hash(OddNumber, R) z.\]However, if the Oracle acts maliciously and modifies the function value to Even, signing CET2 instead
\[s' := k - hash(EvenNumber, R) z.\]then any user can disprove this malicious behavior by demonstrating that
\[f(ξ) ≠ OddNumber.\]3. OP-DLC 2
OP-DLC includes the following five provisions:
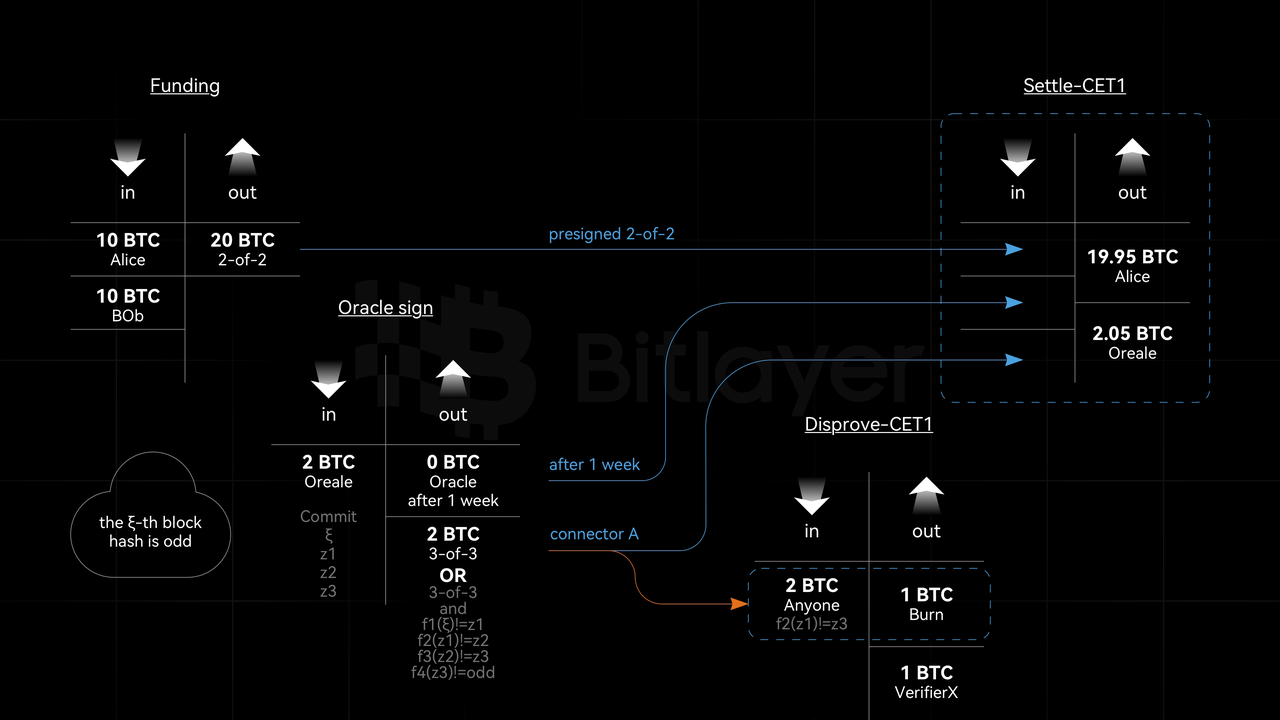
- The Oracle is composed of a federation with n participants, any of whom can sign a CET. Staking 2 BTC is required for the oracle to publish signatures and earn fees. If a member acts maliciously, he loses his stake. Other members can continue to sign CETs, ensuring that users can withdraw funds. Alice and Bob can also become Oracles, thereby achieving true self-reliance and minimizing trust.
- If an Oracle acts maliciously and modifies the results, it will inevitably lead to a situation where f1(ξ) ≠ z1, f2(z1) ≠ z2 etc. Thus, any participant can initiate a challenge by executing a Disprove-CET1 transaction.
- If the Oracle honestly signs the CET, no participant can initiate a valid Disprove transaction. After one week, the CET can be correctly settled. Additionally, the Oracle receives a 0.05 BTC reward for their 2 BTC stake being tied up for one week and for the honest signing of the CET.
- Any participant can challenge the Oracle_sign:
- If Oracle_sign is honest, a Disprove-CET1 transaction cannot be initiated, and the CET settlement will be executed after one week. Furthermore, the Oracle’s stake is unlocked, and receives the fee.
- If Oracle_sign is dishonest, meaning anyone can successfully initiates a Disprove-CET1 transaction and spend the connector A output, then the Oracle’s signature is invalid, and they lose the staked 2 BTC. In the future, that Oracle will not sign the same result for that DLC contract, as the Settle-CET1 relying on connector A output will be permanently invalid.
- The challenge in OP-DLC is permissionless, meaning any participant can supervise whether the contracts within OP-DLC are correctly executed. This minimizes trust in the Oracle. Compared to the Lightning Network, Alice and Bob can also be offline because the CET will only be settled if the Oracle signs honestly, while a malicious Oracle will be challenged and punished by anyone else.
 Advantages:
Advantages:
- High Asset Control and Trust in Oneself: Alice and Bob can both become Oracles and sign CETs. The optimistic challenge mechanism will defeat incorrect CETs, preventing malicious actions. Therefore, OP-DLC allows users to trust only themselves. In BitVM, users need to act as Operators and participate in all subsequent deposits to ensure self-trust. If a user acts as an Operator for only a single UTXO deposit in BitVM, that UTXO can be legally reimbursed by any other (n-1) Operators, meaning the user’s future withdrawals still depend on other Operators to front the funds. BitVM Operator’s reimbursement rights are locked to each individual deposit UTXO.
- High Fund Utilization: If users only trust themselves, the required amount of funds differs. In OP-DLC, users rely on themselves for withdrawals and do not need to front equivalent funds. In BitVM, users need to front equivalent funds and then get reimbursed, which creates greater financial pressure.
- Predefined Signing Oracles: The Oracles capable of signing must be determined at the time of deposit in OP-DLC, but users themselves can also become Oracles, signing for themselves.
Drawbacks:
- Withdrawal Time Requires One Week: Essentially, both OP-DLC and BitVM have the same time cost for funds. OP-DLC withdrawals need to go through a challenge period to access the funds. If BitVM relies on users themselves to front the funds, the equivalent fronted funds also need to go through a challenge period to be successfully reimbursed. If BitVM relies on other Operators to front the funds for quick withdrawal, it means the user must pay the time cost of equivalent funds as a fee to the Operator.
- Rapid Growth in Required Pre-Signed Signatures: The number of required pre-signed signatures grows linearly with the number of CETs. A large number of CETs is needed to enumerate all possible withdrawal outcomes.
4. Conclusion
OP-DLC introduces the optimistic challenge mechanism into CETs to ensure that incorrect CETs are not settled and the malicious Oracle loses its stake, while correct CETs are executed and the Oracle’s stake is unlocked, earning a fee. This method can resist any attack and embodies elegant simplicity.


